golang的container包中提供了heap容器,这个容器可以用来做什么,又是怎么做到的呢?本文从golang 1.9.3的源码出发,说明了堆、heap包、heap包的用途、heap包的实现。
1 heap是什么
首先先来解释一下堆(Heap)是什么。
据维基百科
堆(Heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。在队列中,调度程序反复提取队列中第一个作业并运行,因为实际情况中某些时间较短的任务将等待很长时间才能结束,或者某些不短小,但具有重要性的作业,同样应当具有优先权。堆即为解决此类问题设计的一种数据结构。
逻辑定义:n个元素序列{k1, k2… ki…kn},当且仅当满足下列关系时称之为堆:
(ki <= k2i, ki <= k2i+1)或者(ki >= k2i, ki >= k2i+1), (i = 1, 2, 3, 4... n/2)
堆具有以下特性:
- 任意节点小于(或大于)它的所有后裔,最小元(或最大元)在堆的根上(堆序性)。
- 堆总是一棵完全树。即除了最底层,其他层的节点都被元素填满,且最底层尽可能地从左到右填入。
完全二叉树和满二叉树的区别如下图。
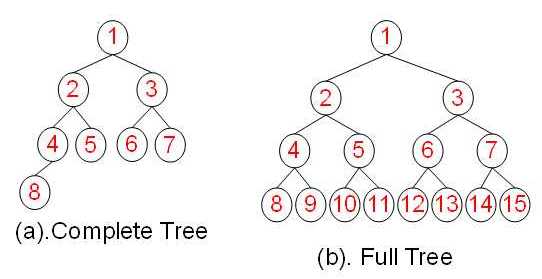
将根节点最大的堆叫做最大堆或大根堆,根节点最小的堆叫做最小堆或小根堆。
由于堆是完全二叉树,所以可以用顺序数组来表示,如下图。
记住这两张图,后面会用到。
2 container/heap提供的方法
了解了堆是什么以后,再来看看container/heap包。
heap包为实现了heap.Interface的类型提供了堆方法:Init/Push/Pop/Remove/Fix。container/heap为最小堆,即每个节点的值都小于它的子树的所有元素的值(A heap is a tree with the property that each node is the minimum-valued node in its subtree)。
type Interface interface {
sort.Interface
Push(x interface{}) // add x as element Len()
Pop() interface{} // remove and return element Len() - 1.
}
由于heap.Interface包含了sort.Interface,所以,目标类型需要包含如下方法:Len/Less/Swap, Push/Pop。
3 container/heap可以用来做什么
container/heap包可以用来构造优先级队列。
以go src的priority queue为例。
定义PriorityQueue类型。
// An Item is something we manage in a priority queue.
type Item struct {
value string // The value of the item; arbitrary.
priority int // The priority of the item in the queue.
// The index is needed by update and is maintained by the heap.Interface methods.
index int // The index of the item in the heap.
}
// A PriorityQueue implements heap.Interface and holds Items.
type PriorityQueue []*Item
func (pq PriorityQueue) Len() int { return len(pq) }
func (pq PriorityQueue) Less(i, j int) bool {
// We want Pop to give us the highest, not lowest, priority so we use greater than here.
return pq[i].priority > pq[j].priority
}
func (pq PriorityQueue) Swap(i, j int) {
pq[i], pq[j] = pq[j], pq[i]
pq[i].index = i
pq[j].index = j
}
func (pq *PriorityQueue) Push(x interface{}) {
n := len(*pq)
item := x.(*Item)
item.index = n
*pq = append(*pq, item)
}
func (pq *PriorityQueue) Pop() interface{} {
old := *pq
n := len(old)
item := old[n-1]
item.index = -1 // for safety
*pq = old[0 : n-1]
return item
}
// update modifies the priority and value of an Item in the queue.
func (pq *PriorityQueue) update(item *Item, value string, priority int) {
item.value = value
item.priority = priority
heap.Fix(pq, item.index)
}
PriorityQueue本质上是个 *Item 数组,其Len/Less/Swap是比较常见的数组用来sort需要定义的函数,而Push、Pop则是使用数组来插入、的方法。PriorityQueue还提供了update方法。注意由于通常希望优先级队列Pop出来的是优先级最高的元素,所以Less方法是反着写的。
定义了以上方法以后,PriorityQueue就具备了使用container/heap包的条件。
如下代码,先从items map出发定义了一个pq数组,长度为hash的size,并调用heap.Init初始化pq数组;之后向队列中增加了一个优先级为1的元素,并更新该元素的队列;最后从队列中依此Pop,可见元素在Pop时是依照优先级排序的。
// This example creates a PriorityQueue with some items, adds and manipulates an item,
// and then removes the items in priority order.
func Example_priorityQueue() {
// Some items and their priorities.
items := map[string]int{
"banana": 3, "apple": 2, "pear": 4,
}
// Create a priority queue, put the items in it, and
// establish the priority queue (heap) invariants.
pq := make(PriorityQueue, len(items))
i := 0
for value, priority := range items {
pq[i] = &Item{
value: value,
priority: priority,
index: i,
}
i++
}
heap.Init(&pq)
// Insert a new item and then modify its priority.
item := &Item{
value: "orange",
priority: 1,
}
heap.Push(&pq, item)
pq.update(item, item.value, 5)
// Take the items out; they arrive in decreasing priority order.
for pq.Len() > 0 {
item := heap.Pop(&pq).(*Item)
fmt.Printf("%.2d:%s ", item.priority, item.value)
}
// Output:
// 05:orange 04:pear 03:banana 02:apple
}
4 heap是怎么做到的
上面举的例子,可以说很神奇了。container/heap是怎么做到的呢?
4.1 heap.Init
先来看看heap.Init函数。
// A heap must be initialized before any of the heap operations
// can be used. Init is idempotent with respect to the heap invariants
// and may be called whenever the heap invariants may have been invalidated.
// Its complexity is O(n) where n = h.Len().
//
func Init(h Interface) {
// heapify
n := h.Len()
for i := n/2 - 1; i >= 0; i-- {
down(h, i, n)
}
}
关键点在于down函数。
func down(h Interface, i0, n int) bool {
i := i0
for {
j1 := 2*i + 1
if j1 >= n || j1 < 0 { // j1 < 0 after int overflow
break
}
j := j1 // left child
if j2 := j1 + 1; j2 < n && h.Less(j2, j1) {
j = j2 // = 2*i + 2 // right child
}
if !h.Less(j, i) {
break
}
h.Swap(i, j)
i = j
}
return i > i0
}
down函数的功能非常简单:给定类型,需要down(下沉)的元素在数组中的索引,heap的长度,将该元素下沉到该元素对应的子树合适的位置,从而满足该子树为最小堆的要求。
还记得前面的那张顺序数组表示堆的图吗?结合down函数的实现:任选一个元素 i ,将其与它的子节点 2i+1 和 2i+2比较,如果元素 i 比它的子节点小,则将元素 i 与两个子节点中较小的节点交换(j),从而保证满足最小树的要求(第一次down);子节点 j 可能也有它的子节点,继续比较、交换,直到数组末尾,或者元素 i 比它的两个子节点都小,跳出循环()。
为什么元素 i 比它的两个子节点都小,就可以跳出循环,不再继续下去呢?这是由于,在Init函数中,第一个开始down(下沉)的元素是第 n/2 - 1 个,可以保证总是从最后一棵子树开始down(如前图,n=8或者n=9, n/2-1总是为4),因此可以保证Init->down时,如果元素 i 比它的两个子节点都小,那么该元素对应的子树,就是最小堆。
Init在遍历完毕后,可以保证,待Init的数组是一个最小堆。
4.2 heap.Push
再来看看heap.Push是怎么保证插入新元素时,顺序数组仍然是一个最小堆。
// Push pushes the element x onto the heap. The complexity is
// O(log(n)) where n = h.Len().
func Push(h Interface, x interface{}) {
h.Push(x)
up(h, h.Len()-1)
}
首先调用h.Push将元素推入用户定义的类型,即前述的PriorityQueue。数组append,没什么好说的。由于是将该元素插入到了数组的末尾位置,所以需要调用up函数来“上浮”。
来看看up是怎么上浮的。
func up(h Interface, j int) {
for {
i := (j - 1) / 2 // parent
if i == j || !h.Less(j, i) {
break
}
h.Swap(i, j)
j = i
}
}
很简单,依此查找元素 j 的父节点(i),如果元素 j 比父节点 i 要小,则交换这两个节点,并继续向再上一级的父节点比较,直到根节点,或者元素 j 大于 父节点 i。
如此,可以保证插入新元素的顺序数组在up之后,仍然是一个最小堆。
4.3 heap.Pop
// Pop removes the minimum element (according to Less) from the heap
// and returns it. The complexity is O(log(n)) where n = h.Len().
// It is equivalent to Remove(h, 0).
func Pop(h Interface) interface{} {
n := h.Len() - 1
h.Swap(0, n)
down(h, 0, n)
return h.Pop()
}
前面PriorityQueue的Pop函数,实际是取了顺序数组的 :n-1 子数组,因此heap.Pop的目的就是将根节点(0)与末尾节点的元素交换,并将新的根节点的元素down(下沉)到合适的位置,满足最小堆的要求;最后再调用PriorityQueue的Pop函数获取最后一个元素即可。
4.4 heap.Fix
PriorityQueue的update函数在修改元素优先级的时候,实际是靠heap.Fix完成的。
// Fix re-establishes the heap ordering after the element at index i has changed its value.
// Changing the value of the element at index i and then calling Fix is equivalent to,
// but less expensive than, calling Remove(h, i) followed by a Push of the new value.
// The complexity is O(log(n)) where n = h.Len().
func Fix(h Interface, i int) {
if !down(h, i, h.Len()) {
up(h, i)
}
}
代码比较清晰:如果能下沉,则下沉,否则上浮。down的返回值可以表达是否有下沉过(即是否有swap过)。
4.5 heap.Remove
优先级队列的示例中没有使用Remove函数,直接来看代码。
// Remove removes the element at index i from the heap.
// The complexity is O(log(n)) where n = h.Len().
//
func Remove(h Interface, i int) interface{} {
n := h.Len() - 1
if n != i {
h.Swap(i, n)
if !down(h, i, n) {
up(h, i)
}
}
return h.Pop()
}
先将要删除的节点 i 与末尾节点 n 交换,然后将新的节点 i 下沉或上浮到合适的位置。这块逻辑跟Fix是类似的,但注意不能直接调用heap.Fix,最后一个元素是要被删除的,不能参与Fix。
Ref:






