今天终于知道 Redis 为什么要用跳跃表了

> 放低心态、认真学习，机会总是留给不断努力的自己 本篇说下跳表，首先，Redis 中的有序集合(Sorted Set)就是用跳表（Skip list）来实现的。 如果你了解过平衡二叉树，应该知道红黑树也可以实现快速的插入、删除和查找操作。那 **Redis** 为什么会选择用跳表来实现有序集合呢? 为什么不用红黑树呢?学完今天的内容，你就知道答案了。 ### 1. 什么是跳表 先说一下单链表，是一种各性能比较优秀的动态数据结构，可以支持快速的插入、删除、查找操作。  对于一个单链表来讲，即便链表中存储的数据是有序的，如果我们要想在其中查找某个数据，也只能从头到尾遍历链表。这样查找效率就会很低，时间复杂度会很高，是O(n)。 那怎么来提高查找效率呢？如果像上图中那样，对链表建立一级“索引”，查找起来是不是就会更快一些呢?每两个结点提取一个结点到上一级，我们把抽出来的那 一级叫作索引或索引层。你可以看我画的图。图中的down表示指针，指向下一级结点。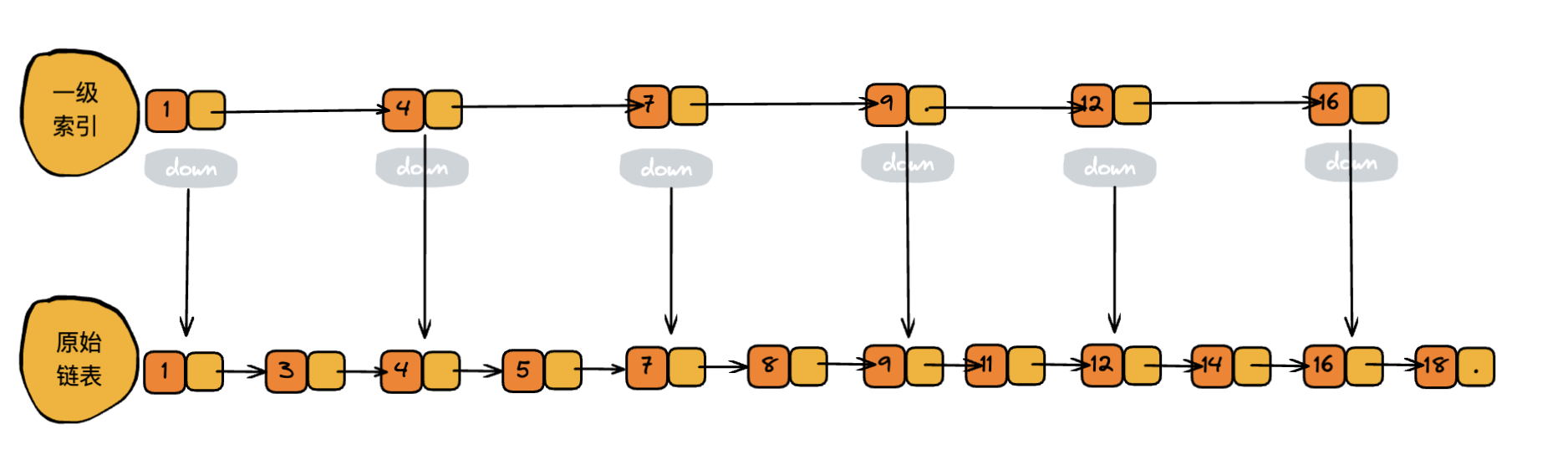  如果我们要查找某一个结点，比如 14，遍历第一级索引层，到 12 的时候下一个结点是 16，那查找的目标 14 就一定在这 2 个结点之间。然后通过 down 指针，找到原始链表这层遍历，此时只需要遍历 2 个结点就能找到目标结点 14 了，这样我们就实现了查找。整个过程只需要遍历 7 个结点就能找到，原先需要 10 个结点。 从中能看出，我们加了一级索引层，需要遍历的结点数相对于原来大大的减少了，提高了查找的效率 。如果我们在加一个二级索引层，在查找效率上会不会更加的提升呢? 答案是肯定的。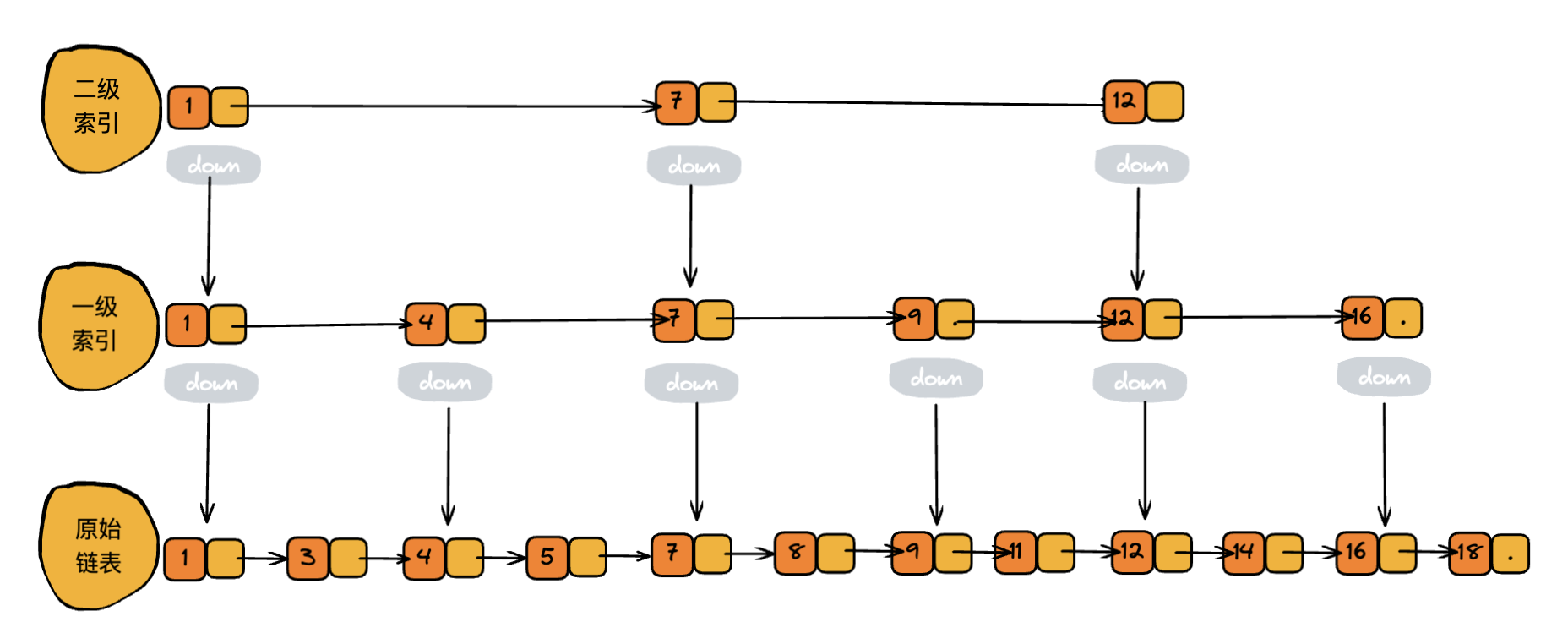  由于列子结点较少，可能未很好的表达。查找效率提升不明显，我增加一个 64 个结点的链表，构建了一个五级引层。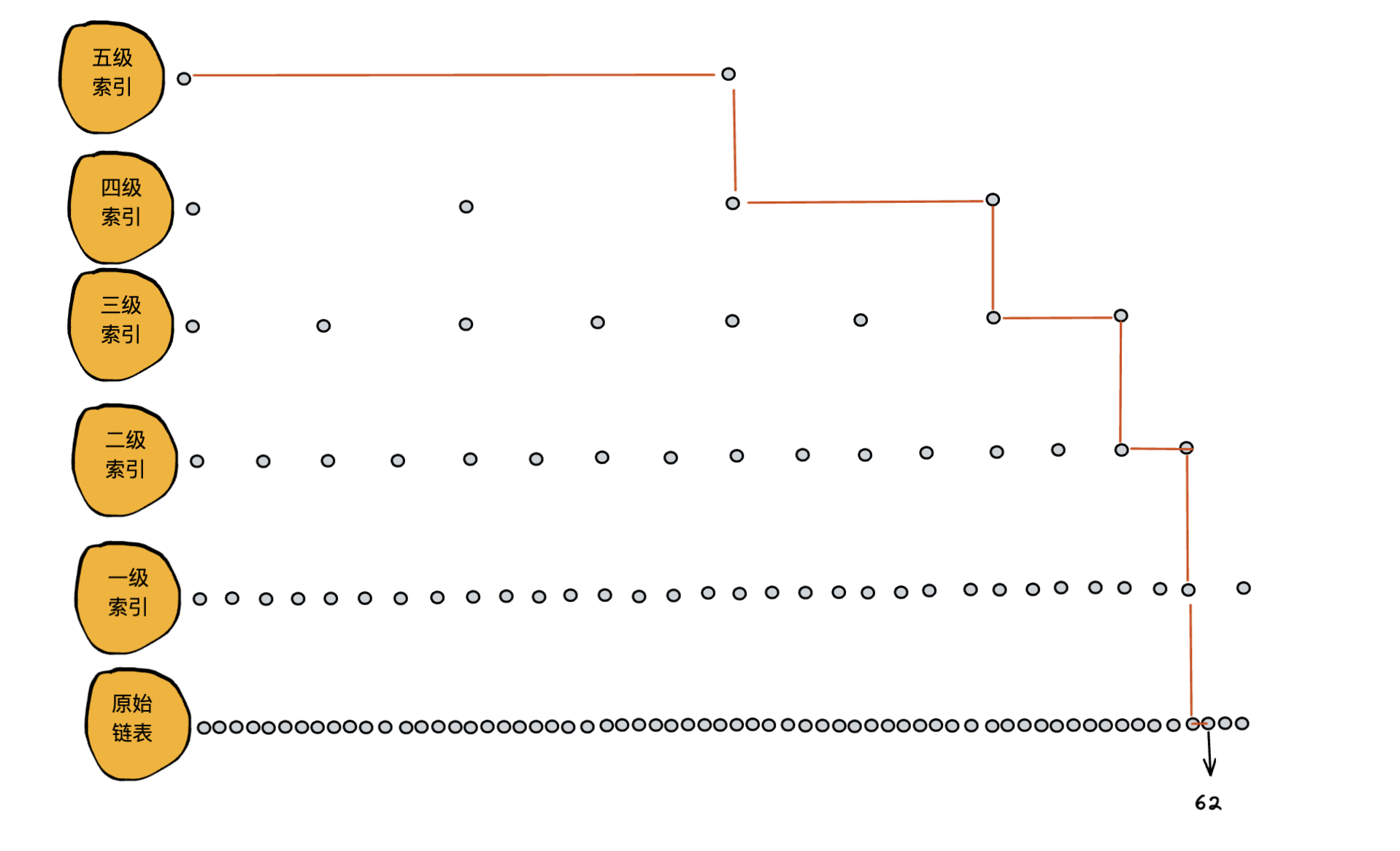 从上图可以发现，查找 62 没有用索引的情况，要遍历 62 次个结点才能找到，现在只需要 11 个结点就能找到，效率提高很明显。所以，当链表长度越长，在构建索引后，查找效率提高越发的明显。 以上这种加多级索引的数据结构就称为跳表。跳表是能够提升查询效率的。接下来说下用跳表到底有多快。 ### 2. 跳表有多快 一个单链表查询数据的时间复杂度是 `O(n)`，多级索引的跳表呢？ 分析一下：n 个结点的链表，每 2 个结点会抽出 1 个结点作为上一级的一个结点，则第一级索引有 n/2 个结点，第二级索引 n/4 个结点，第三级 n/8 ... 所以，第 J 级索引结点的个数是 J-1 级的 1/2 ，则第 J 级结点的个数就是 n/(2J) 。 若索引有 h 级，最顶层的索引有 2 个结点，我们可以得到 `n/(2h)=2`, 则 `h=log2n-1`。 加上低层原始链表这一层，整个跳表结构的高度就是 log2n。 当我们查询数据时，若每层都需要遍历 m 个结点，那么在跳表中查询一个数据的时间复杂度就是 `O(m*logn)`。那么 m 为多少呢？ 我们每一级都需要遍历 3 个结点，也就是说 m=3， 为什么是 3 ？ 若我们要查找的数据是 x，在第 J 级索引中，我们遍历到 y 结点，发现 x 大于 y，小于后面的结点 z，所以通过 y 的指针（down），从第 J 级索引下降到第 J-1 级索引。在第 J-1 索引中，y 和 z 中只有 3 个结点（包含 y 和 z）。索引，在 J - 1 级索引中查找书籍只需要遍历 3 个结点，所以，也就是每一级索引都最多只需要遍历 3 个结点。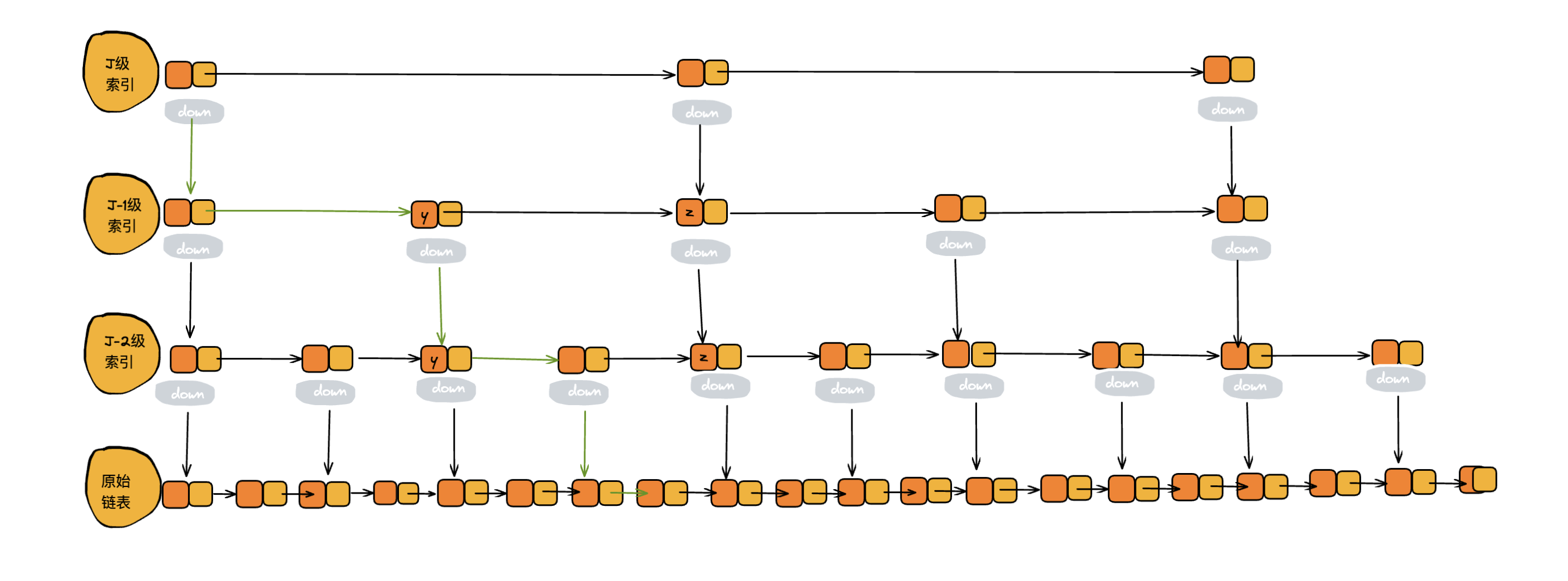  通过上面的分析，得到 m=3，所以在跳表中查询任意数据的时间复杂度就是 `O(logn)`。从中可以看出为了提升查询效率的提升，建立了很多索引层，典型的空间换时间。 ### 3. 跳表是否浪费内存 上面说了，跳表为了提高查找的效率，采用了空间换时间的方案，那么到底需要消耗多少储存的空间。我们分析一下跳表的空间复杂度。 假设原始的链表大小为 n，第一级索引的有 n/2 个结点，妹上升一级就减少一半，一直到顶层只有 2 个结点。 $$ \frac{n}{2}\ , \frac{n}{4}\ , \frac{n}{8}\ ..., 8, 4, 2 $$ 没错上面这个就是等比数列，所以跳表的空间复杂度就是 `O(n)`。 ### 4、动态插入和删除 现在，大家应该有印象跳表是一个什么样的数据结构了把，跳表不仅支持查找、还支持动态的插入和删除。 我们知道，单链表的插入复杂度是`O(1)`, 但是需要遍历所有的结点才能找到插入的位置，这个查找的过程是非常耗时的，对于跳表来说找到插入的的位置是很快的，时间复杂度是 `O(logn)`。看下插入的过程。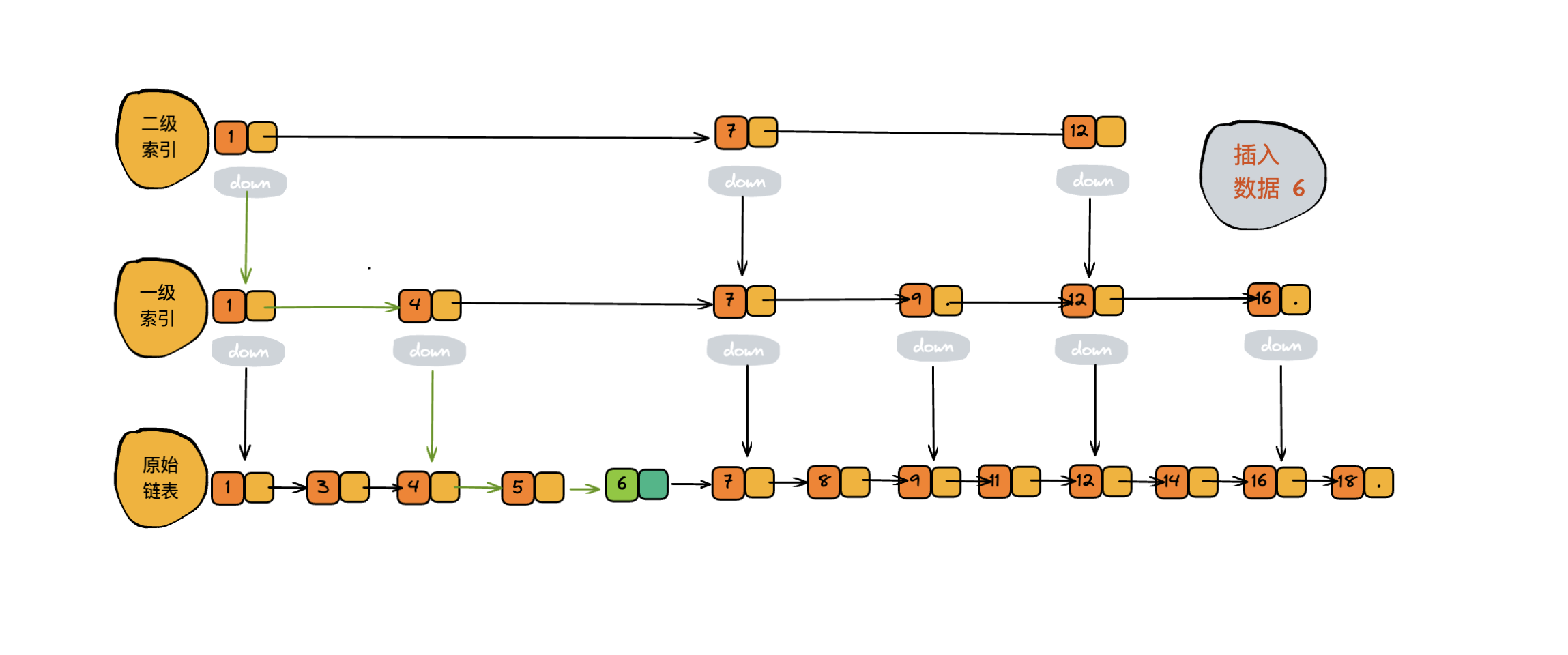插入一个 6 的过程：  删除操作： 若删除的结点在索引中，我们需要删除原始链表中的结点，还要删除索引的结点。单链表中删除一个数据时需要拿到该结点的前驱结点，然后通过指针删除。所以需要找到删除的结点，一定要获取前驱结点。双向链表不需要这个操作。 ### 5. 跳表索引更新 从上面插入数据 6 的过程中发现，我们插入6时没有更新索引，会出现 2 个索引结点之间数据非常多的情况，若频繁的插入数据，但不更新索引，最终会退化成单链表的数据结构，会导致查找数据效率变低。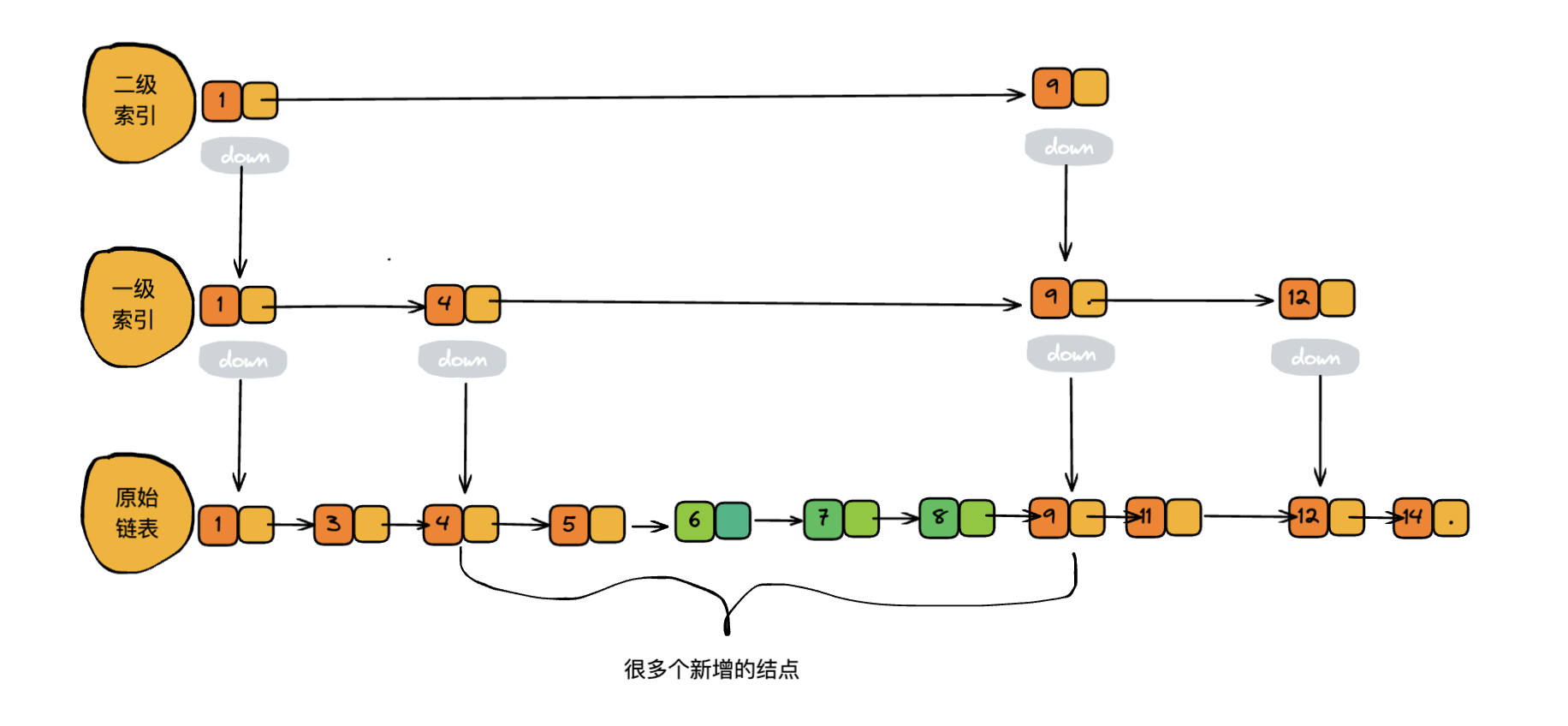如下图：  跳表作为一个动态的数据结构，需要动态的维护索引与原始链表中的大小。若原始链表插入的结点变多了，那么相应的索引结点也需要增加，避免查找、删除、插入的性能下降。 如 AVL 树、红黑树。他们是通过左右旋的方式保证左右子树平衡的（若不了平衡二叉树，后面会说），而跳表是通过随机函数来保证 ”平衡性“的。 那么插入数据时，如何选择要插入到哪个索引层的呢？ 其实是通过一个随机函数，来决定将这个结点插入到哪几级索引中，比如随机函数生成了值K，那就将这个结点添加到第一级到第K级这K级索引中。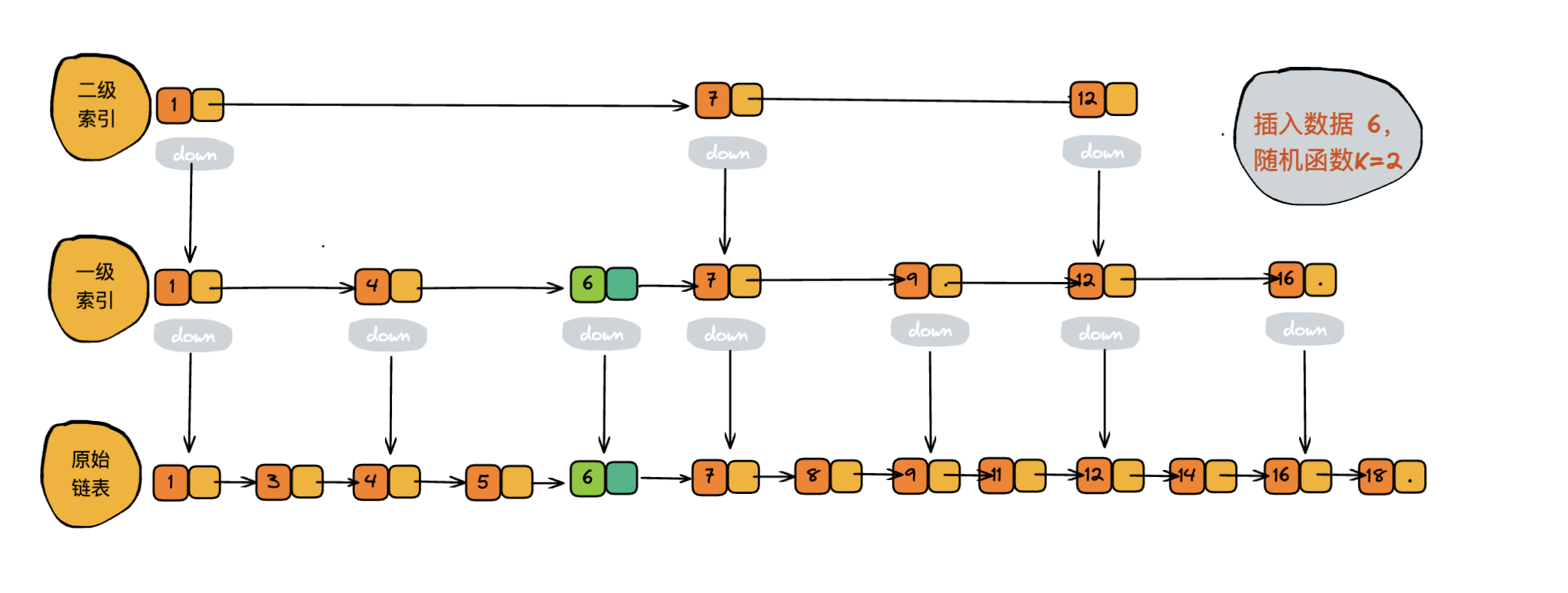  能够保证跳表的索引大小和数据大小平衡性，保证在插入、删除、查找中性能不退化。至于随机函数的选择，我就不展开讲解了。有兴趣的可以查阅一下资料或者看下 Redis 源码。 ### 6. 总结 本篇讲了跳表这种动态数据结构。通过构建多级索引来提高查询的效率，使用了空间换时间的思路。支持高效的查找、删除、插入数据操作，时间复杂度都是 `O(logn)`、空间复杂度 `O(n)`。跳表的设计思想非常的高效，在实现上非常灵活，通过随机函数动态构建索引层。相比其他的平衡二叉树，在实现上简单很多。 Redis 在实现有序集合时选择了跳表实现，非常的高效。 > 题外话：最近大厂裁员的消息很多，要从现在开始准备起来！关注一下不迷路，感谢兄弟们。 欢迎关注微信公众号：【程序员祝融】一起交流学习！原文链接：https://mp.weixin.qq.com/s/ptyTt7aGj5-UrQdvc98v2A