1. 首页
  2. 文章

红黑树原理详解及golang实现

ailumiyana · · 1419 次点击 · · 开始浏览    
这是一个创建于 的文章，其中的信息可能已经有所发展或是发生改变。
第一次，站长亲自招 Gopher 了>>>

目录

红黑树原理详解及golang实现

在看红黑树原理之前，先看下二叉查找树。

二叉查找树

二叉查找树，又称二叉排序树，二叉搜索树。

性质

它具备一下性质：

1、左子树上的所有节点均小于它的根节点值。
2、右子树上的所有节点的值均大于等于它根节点的值。
3、左佑子树也分别二叉排序树。
4、没有键值相等的节点。

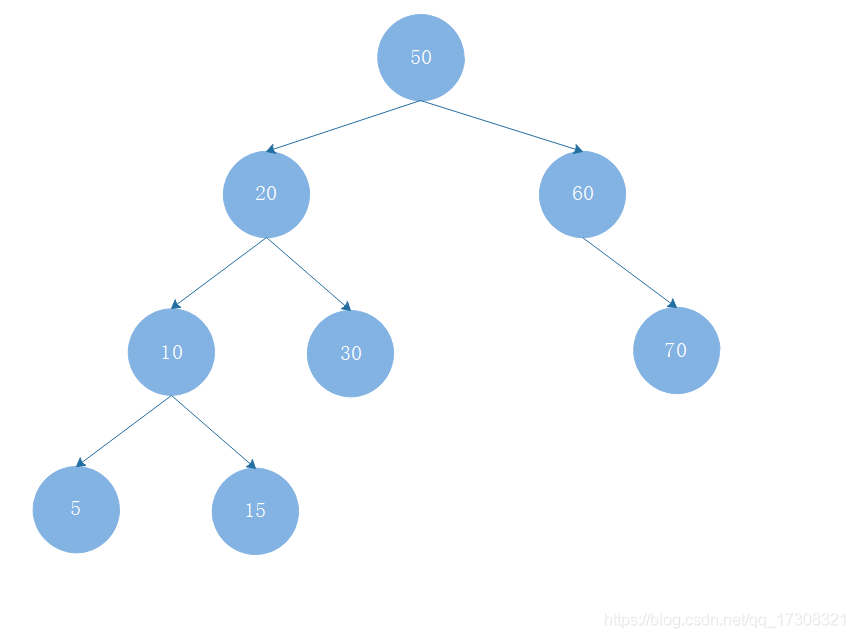
Alt text

既然叫搜索树，那这种结构的好处当然也就是搜索咯，
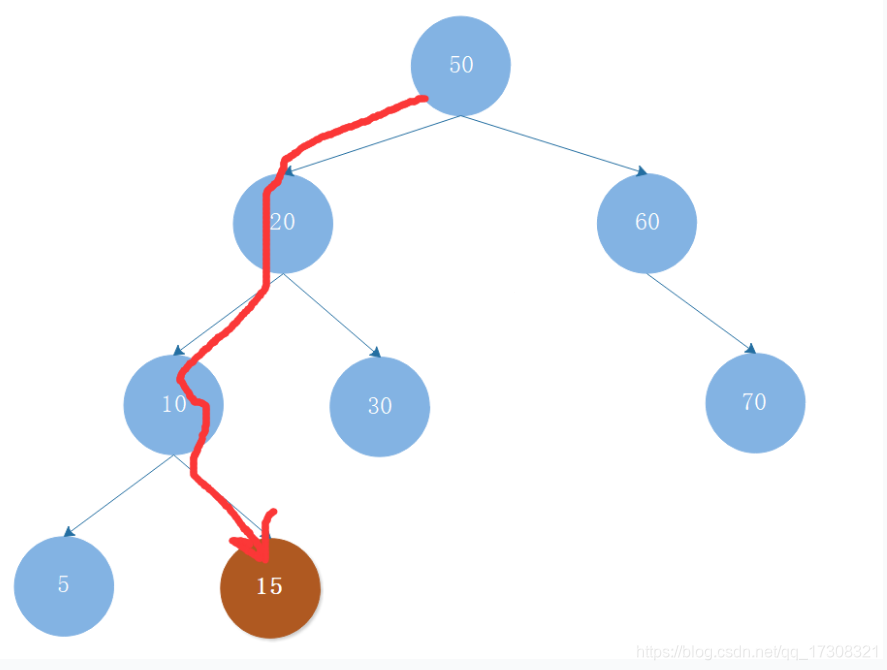
假如我们要查找15

1、从root节点开始，15<50，找左子树。
2、15<20，找左子树，
3、15>10，找右子树，这样便找到15了。

插入也是类似方法，一层一层比较大小，找到合适的位置插入。
在这里插入图片描述

时间复杂度
看见它查找的次数等同于树的高度，在最好的情况下，其平均查找次数和log 2 (n)成正比。
当然也有坏情况，当先后插入的关键字有序时，构成的二叉排序树蜕变为单支树，树的深度和其节点数成正比(和顺序查找相同）.
例如依序插入 ： 100、200、90、80、70、60、50、40
就会成为如下图形态：
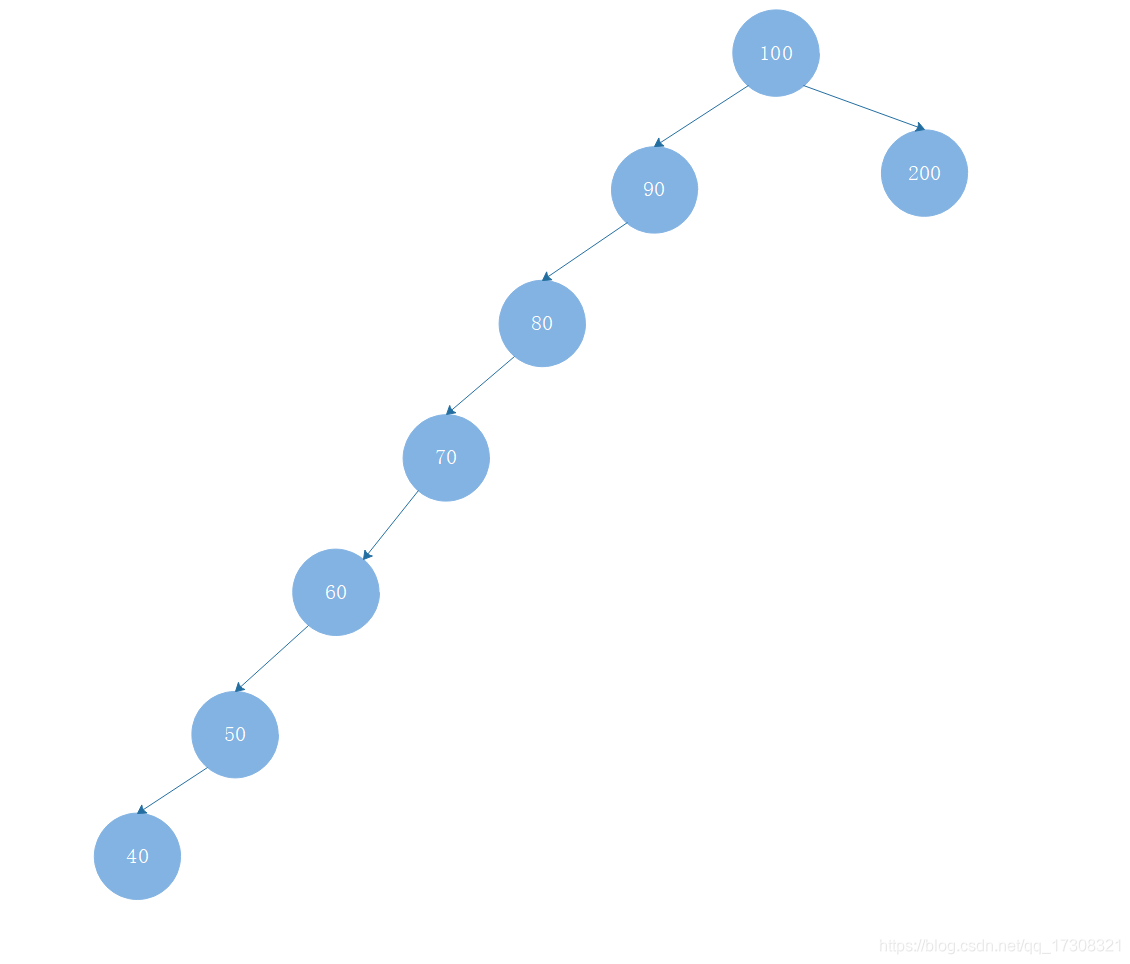
Alt text

为了解决这种不平衡的情形，就有了红黑树。

红黑树

性质

红黑树是一种自平衡的二叉搜索树，它包含了二叉搜索树的特性，同时具备以下性质：

1、所有节点的颜色不是红色就是黑色。
2、根节点是黑丝。
3、每个叶子节点都是黑色的空节点(nil)。
4、每个红色节点的两个子节点都是黑色。(从每个叶子到根节点的所有路径上不能有两个连续的红色节点)
5、从任一节点到其叶子节点的所有路径上都包含相同数目的黑节点。

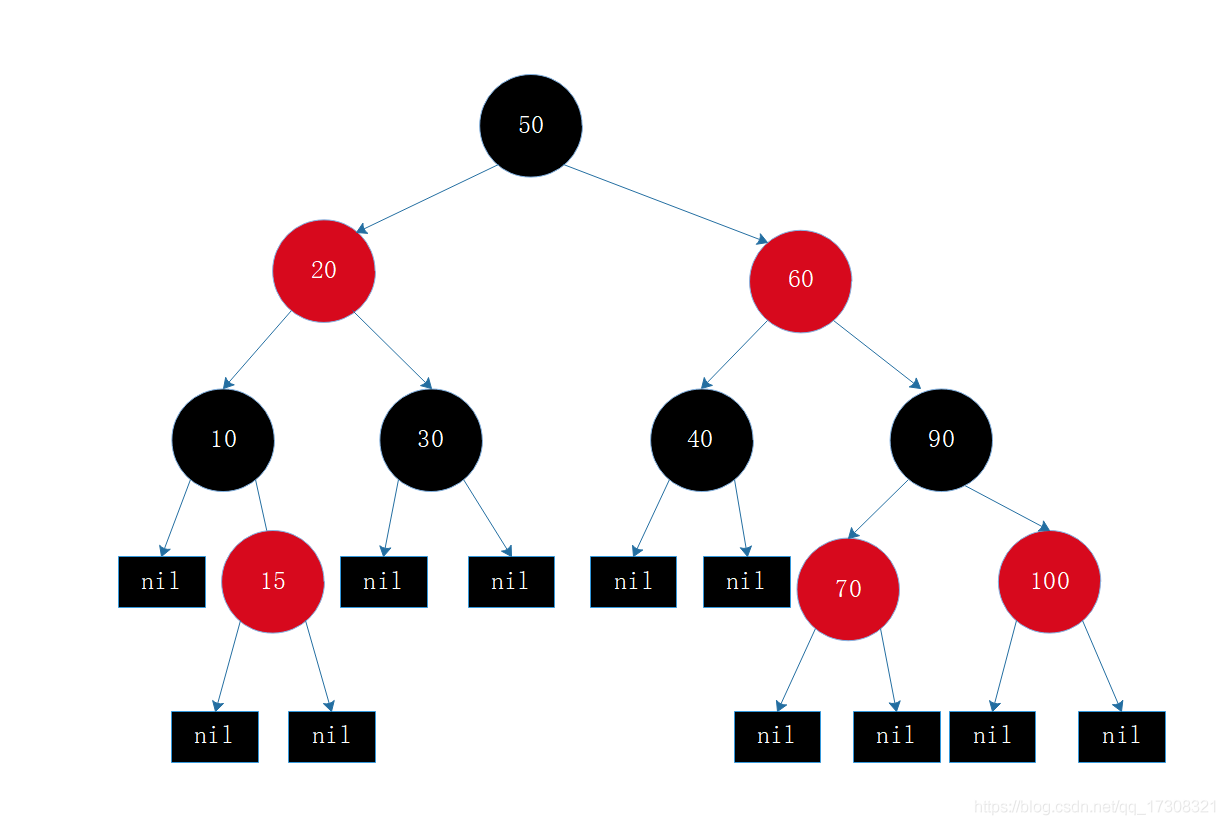
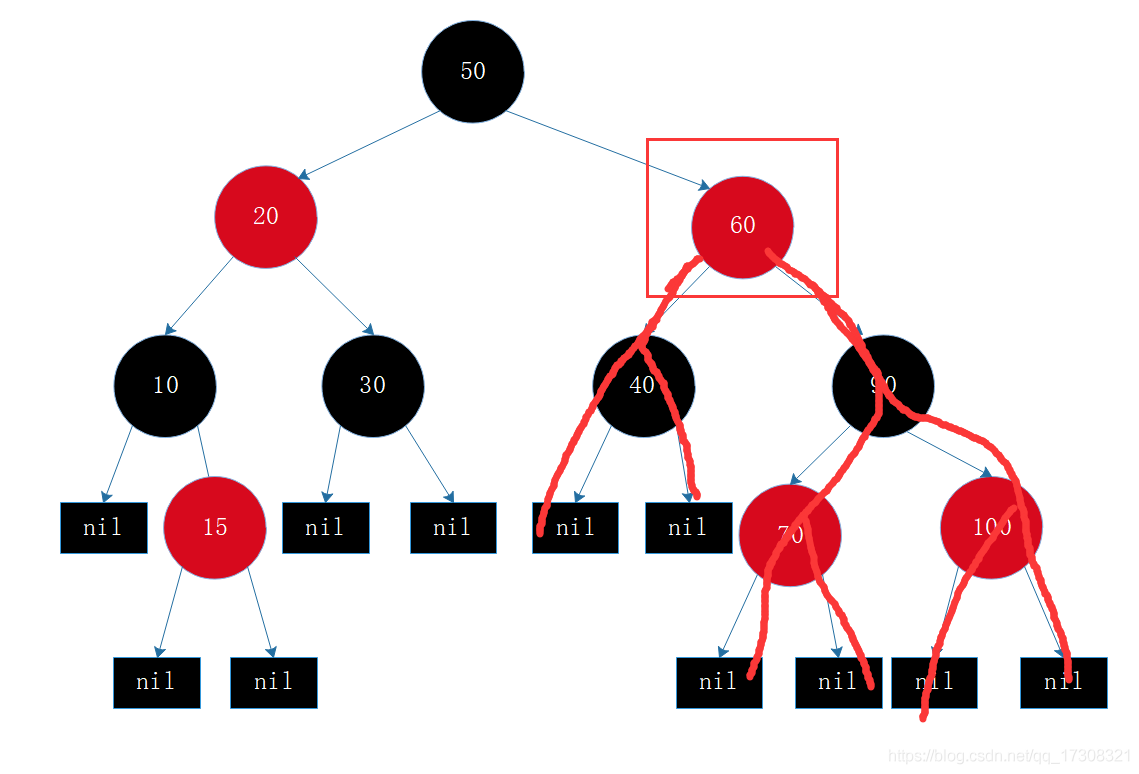
Alt text

前四都能理解其意思吧，所以只解释下第五点，比如60这个节点，到其所有叶子节点的路径都只包含1个黑色节点：40和90。

Alt text

operation

红黑树为了维持它的这5点性质，于是它支持了这么几个操作 ，

变色 ： 顾名思义变色，红变黑，黑变红。
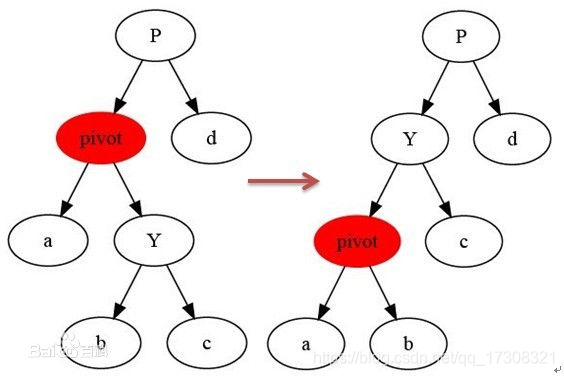
左旋转 : 这里借用百度百科两张旋转图，以图中红色节点为中心，中心节点为右孩子替代，而自己成为它的左孩子，同时节点b作为pivot的有孩子(至于为什么是右孩子，b原本就在pivot的右子树上，所以肯定大于pivot)。
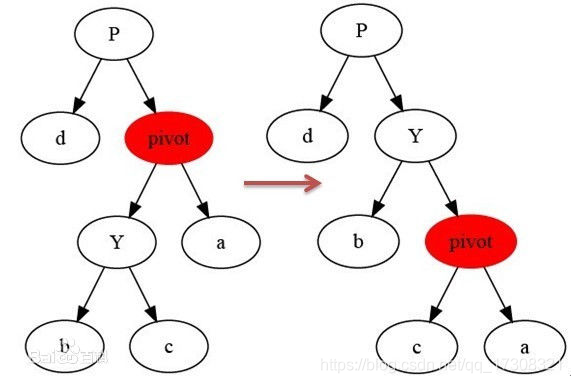
Alt text

右选装 : 同左旋转，中心点顺时钟旋转，成为其原来左孩子的右孩子，原来左孩子的右孩子则成为原中心点的左孩子。
Alt text

接着看看红黑树的插入，看看它是如何通过这几个op维持红黑树这5个性质的。

红黑树的插入

关于插入的特点 ： 由于性质5的约束，每次插入的节点颜色必然为红色。

插入的化存在几种情形，复杂的树可能会涉及到循环的向树上检索做自平衡，这里先从一颗空树开始先简单理解下这些情形。

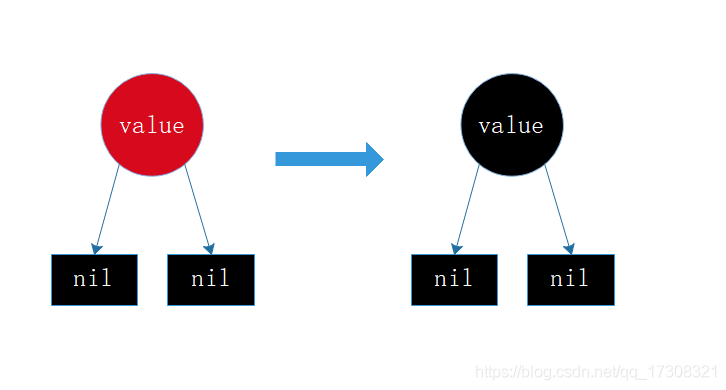
情形1：空树

直接插入，直接作为根节点，同时由于性质1的约束，通过变色op变为黑色即可。

Alt text

情形2：插入节点父节为黑色，

不违反任何性质，无需做任何修改。

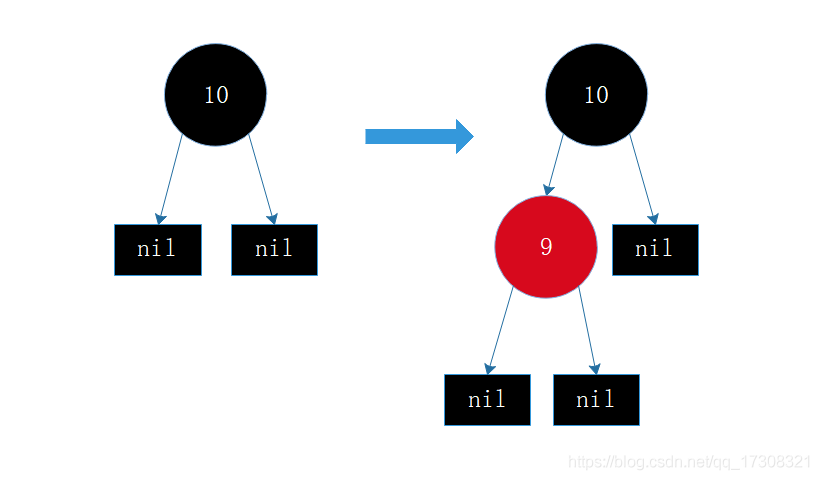
Alt text

情形3 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为左孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为右孩子)。

这是一种插入节点和父节点在一个方向上的情况(例如父节点为左孩子，插入节点也为左孩子)和情形5相反

父节点 及 父父节点变色，在进行左/右旋转， 具体做还是右看你插入的节点的父节点是左子树还是右子树，图例为左子树。

此处 : 变色 - > 右旋转

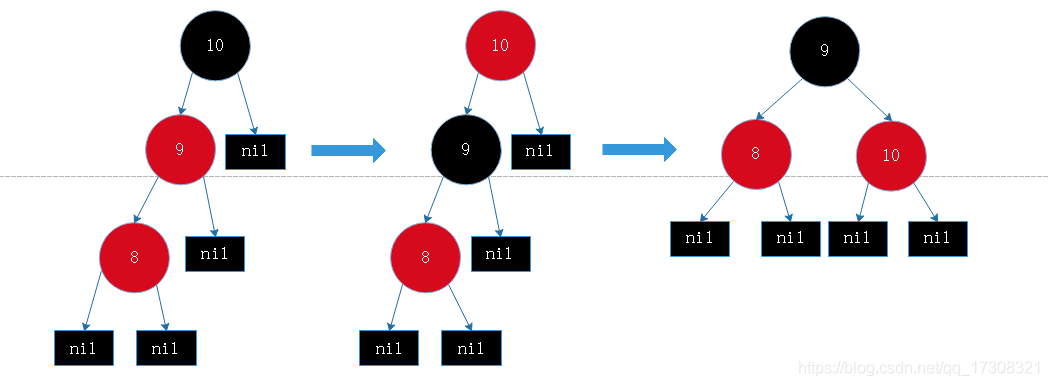
Alt text

情形4 插入节点父节点为红色，父父节点的左/右孩子为红色

先将父节点和父父节点右孩子变黑，父父节点变红，然后将父节点当做插入节点一样递归向上进行平衡红黑树性质操作。 若父节点为根节点直接变父节点为黑色即可.

此处 : 变色 -> 变色

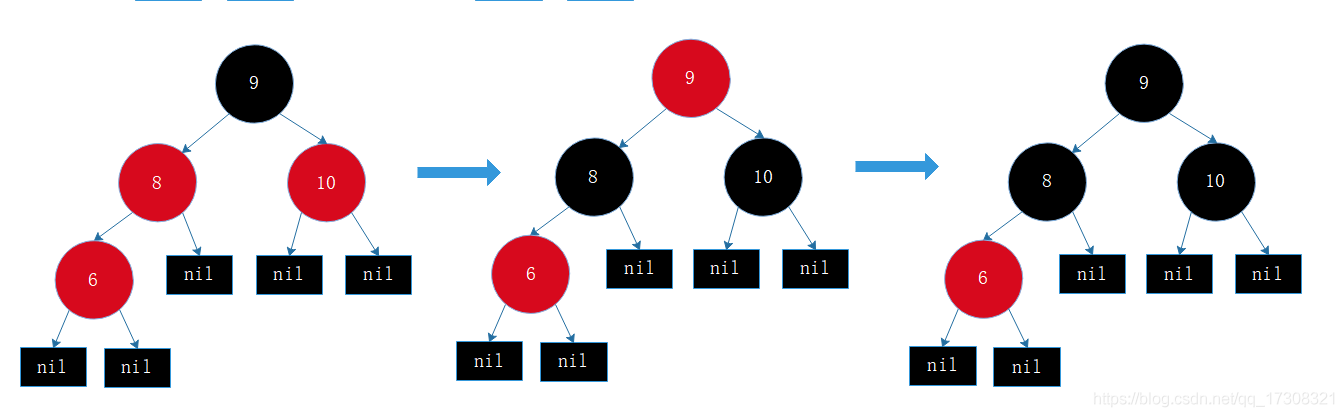
Alt text

情形5 插入节点的父节点为红色，父节点为父父节点的左孩子，父父节点的右孩子为黑色，插入节点为右孩子(或者父节点为父父节点的右孩子，父父节点的左孩子为黑色，插入节点为左孩子)。

和情形3类比是一种反向情况，这种情况进行两次旋转，
先左/右旋转，旋转后变成了情形3，接着按情形3变换即可。

此处 ：左旋转 -> 变色 -> 右旋转
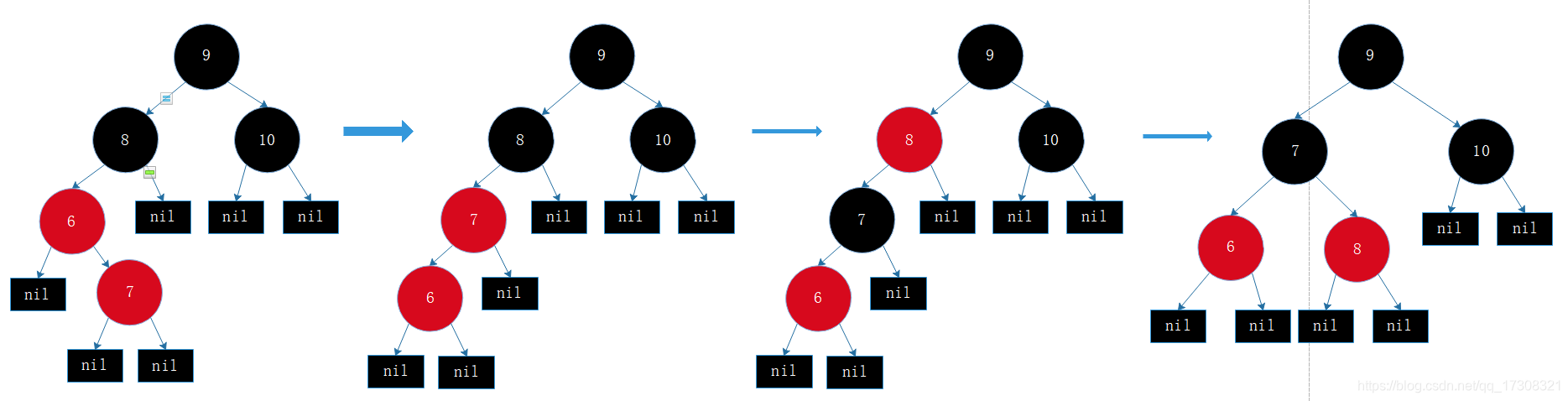
Alt text

golang实现

类型定义

需要注意的是 红黑树的NIL节点需要单独定义出来，不能直接用nil哦。

const (
    RED = true
    BLACK = false
)

type Node struct {
    Parent *Node
    Left   *Node
    Right  *Node
    color  bool
    Item
}

type Rbtree struct {
    NIL  *Node
    root *Node
    count uint64
}

func New() *Rbtree{
    node := Node{nil, nil, nil, BLACK, nil}
    return &Rbtree{
        NIL   : &node,
        root  : &node,
        count : 0,
    }
}

leftRotate

// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
    // Since we are doing the left rotation, the right child should *NOT* nil.
    if no.Right == nil {
        return
    }

    //          |                                  |
    //          X                                  Y
    //         / \         left rotate            / \
    //        α  Y       ------------->         X   γ
    //           / \                            / \
    //          β  γ                            α  β

    rchild := no.Right
    no.Right = rchild.Left

    if rchild.Left != nil {
        rchild.Left.Parent = no
    }

    rchild.Parent = no.Parent

    if no.Parent == nil {
        rbt.root = rchild
    } else if no == no.Parent.Left {
        no.Parent.Left = rchild
    } else {
        no.Parent.Right = rchild
    }

    rchild.Left = no

    no.Parent = rchild

}

func LeftRotateTest(){
    var i10 Int = 10
    var i12 Int = 12

    rbtree := New()
    x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
    rbtree.root = x
    y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
    rbtree.root.Right = y

    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

    rbtree.LeftRotate(rbtree.root)
    
    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

}

Alt text

RightRotate

// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
    if no.Left == nil {
        return
    }

    //          |                                  |
    //          X                                  Y
    //         / \         right rotate           / \
    //        Y   γ      ------------->         α  X
    //       / \                                    / \
    //      α  β                                    β  γ

    lchild := no.Left
    no.Left = lchild.Right

    if lchild.Right != nil {
        lchild.Right.Parent = no
    }

    lchild.Parent = no.Parent

    if no.Parent == nil {
        rbt.root = lchild
    } else if no == no.Parent.Left {
        no.Parent.Left = lchild
    } else {
        no.Parent.Right = lchild
    }

    lchild.Right = no

    no.Parent = lchild

}

func RightRotateTest(){
    var i10 Int = 10
    var i12 Int = 12

    rbtree := New()
    x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
    rbtree.root = x
    y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
    rbtree.root.Right = y

    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

    rbtree.RightRotate(rbtree.root)
    
    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

}

Alt text

Item Interface

值类型接口

type Item interface {
    Less(than Item) bool
}

type Int int

func (x Int) Less(than Item) bool {
    log.Println(x, " ", than.(Int))
    return x < than.(Int)
}

type Uint32 uint32

func (x Uint32) Less(than Item) bool {
    log.Println(x, " ", than.(Uint32))
    return x < than.(Uint32)
}

type String string

func (x String) Less(than Item) bool {
    log.Println(x, " ", than.(String))
    return x < than.(String)
}

func ItemTest(){
    var itype1 Int = 10
    var itype2 Int = 12

    log.Println(itype1.Less(itype2))


    var strtype1 String = "sola"
    var strtype2 String = "ailumiyana"

    log.Println(strtype1.Less(strtype2))
}

Alt text

insert

func (rbt *Rbtree) Insert(no *Node) {
    x := rbt.root
    var y *Node = rbt.NIL

    for x != rbt.NIL {
        y = x 
        if less(no.Item, x.Item) {
            x = x.Left
        } else if less(x.Item, no.Item) {
            x = x.Right
        } else {
            log.Println("that node already exist")
        }
    }

    no.Parent = y
    if y == rbt.NIL {
        rbt.root = no
    } else if less(no.Item, y.Item) {
        y.Left = no
    } else {
        y.Right = no
    }

    rbt.count++
    rbt.insertFixup(no)

}

func (rbt *Rbtree) insertFixup(no *Node) {
    for no.Parent.color == RED {
        if no.Parent == no.Parent.Parent.Left {
            y := no.Parent.Parent.Right
            if y.color == RED {
                //
                // 情形 4

                log.Println("TRACE Do Case 4 :", no.Item)

                no.Parent.color = BLACK
                y.color = BLACK
                no.Parent.Parent.color = RED
                no = no.Parent.Parent  //循环向上自平衡.
            } else {
                if no == no.Parent.Right {
                    //
                    // 情形 5 : 反向情形
                    // 直接左旋转 , 然后进行情形3(变色->右旋)
                    log.Println("TRACE Do Case 5 :", no.Item)

                    if no == no.Parent.Right {
                        no = no.Parent
                        rbt.LeftRotate(no)
                    }
                }
                log.Println("TRACE Do Case 6 :", no.Item)

                no.Parent.color = BLACK
                no.Parent.Parent.color = RED
                rbt.RightRotate(no.Parent.Parent)
            }
        } else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
            y := no.Parent.Parent.Left
            if y.color == RED {
                no.Parent.color = BLACK
                y.color = BLACK
                no.Parent.Parent.color = RED
                no = no.Parent.Parent
            } else {
                if no == no.Parent.Left {
                    no = no.Parent
                    rbt.RightRotate(no)
                }
                
                no.Parent.color = BLACK
                no.Parent.Parent.color = RED
                rbt.LeftRotate(no.Parent.Parent)
            }
        }
    }
    rbt.root.color = BLACK
}

func InsertTest(){
    rbtree := New()

    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})

    log.Println("rbtree counts : ", rbtree.count)

    log.Println("------ ", rbtree.root.Item)
    log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
    log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)

}

InsertTest() 仔细瞧瞧这就是我们 讲情形那棵树 哈 。

Alt text

完整代码

package main

import(
    "log"
)

const (
    RED = true
    BLACK = false
)

//-----------------------------------
//Item interface
//
type Item interface {
    Less(than Item) bool
}

type Int int

func (x Int) Less(than Item) bool {
    log.Println(x, " ", than.(Int))
    return x < than.(Int)
}

type Uint32 uint32

func (x Uint32) Less(than Item) bool {
    log.Println(x, " ", than.(Uint32))
    return x < than.(Uint32)
}

type String string

func (x String) Less(than Item) bool {
    log.Println(x, " ", than.(String))
    return x < than.(String)
}

//-----------------------------------

type Node struct {
    Parent *Node
    Left   *Node
    Right  *Node
    color  bool
    Item
}

type Rbtree struct {
    NIL  *Node
    root *Node
    count uint64
}

func New() *Rbtree{
    node := &Node{nil, nil, nil, BLACK, nil}
    return &Rbtree{
        NIL   : node,
        root  : node,
        count : 0,
    }
}

func less(x, y Item) bool {
    return x.Less(y)
}

// Left Rotate
func (rbt *Rbtree) LeftRotate(no *Node) {
    // Since we are doing the left rotation, the right child should *NOT* nil.
    if no.Right == rbt.NIL {
        return
    }

    //          |                                  |
    //          X                                  Y
    //         / \         left rotate            / \
    //        α  Y       ------------->         X   γ
    //           / \                            / \
    //          β  γ                            α  β

    rchild := no.Right
    no.Right = rchild.Left

    if rchild.Left != rbt.NIL {
        rchild.Left.Parent = no
    }

    rchild.Parent = no.Parent

    if no.Parent == rbt.NIL {
        rbt.root = rchild
    } else if no == no.Parent.Left {
        no.Parent.Left = rchild
    } else {
        no.Parent.Right = rchild
    }

    rchild.Left = no

    no.Parent = rchild

}

// Right Rotate
func (rbt *Rbtree) RightRotate(no *Node) {
    if no.Left == rbt.NIL {
        return
    }

    //          |                                  |
    //          X                                  Y
    //         / \         right rotate           / \
    //        Y   γ      ------------->         α  X
    //       / \                                    / \
    //      α  β                                    β  γ

    lchild := no.Left
    no.Left = lchild.Right

    if lchild.Right != rbt.NIL {
        lchild.Right.Parent = no
    }

    lchild.Parent = no.Parent

    if no.Parent == rbt.NIL {
        rbt.root = lchild
    } else if no == no.Parent.Left {
        no.Parent.Left = lchild
    } else {
        no.Parent.Right = lchild
    }

    lchild.Right = no

    no.Parent = lchild

}

func (rbt *Rbtree) Insert(no *Node) {
    x := rbt.root
    var y *Node = rbt.NIL

    for x != rbt.NIL {
        y = x 
        if less(no.Item, x.Item) {
            x = x.Left
        } else if less(x.Item, no.Item) {
            x = x.Right
        } else {
            log.Println("that node already exist")
        }
    }

    no.Parent = y
    if y == rbt.NIL {
        rbt.root = no
    } else if less(no.Item, y.Item) {
        y.Left = no
    } else {
        y.Right = no
    }

    rbt.count++
    rbt.insertFixup(no)

}

func (rbt *Rbtree) insertFixup(no *Node) {
    for no.Parent.color == RED {
        if no.Parent == no.Parent.Parent.Left {
            y := no.Parent.Parent.Right
            if y.color == RED {
                //
                // 情形 4

                log.Println("TRACE Do Case 4 :", no.Item)

                no.Parent.color = BLACK
                y.color = BLACK
                no.Parent.Parent.color = RED
                no = no.Parent.Parent  //循环向上自平衡.
            } else {
                if no == no.Parent.Right {
                    //
                    // 情形 5 : 反向情形
                    // 直接左旋转 , 然后进行情形3(变色->右旋)
                    log.Println("TRACE Do Case 5 :", no.Item)

                    if no == no.Parent.Right {
                        no = no.Parent
                        rbt.LeftRotate(no)
                    }
                }
                log.Println("TRACE Do Case 6 :", no.Item)

                no.Parent.color = BLACK
                no.Parent.Parent.color = RED
                rbt.RightRotate(no.Parent.Parent)
            }
        } else { //为父父节点右孩子情形，和左孩子一样，改下转向而已.
            y := no.Parent.Parent.Left
            if y.color == RED {
                no.Parent.color = BLACK
                y.color = BLACK
                no.Parent.Parent.color = RED
                no = no.Parent.Parent
            } else {
                if no == no.Parent.Left {
                    no = no.Parent
                    rbt.RightRotate(no)
                }
                
                no.Parent.color = BLACK
                no.Parent.Parent.color = RED
                rbt.LeftRotate(no.Parent.Parent)
            }
        }
    }
    rbt.root.color = BLACK
}

func LeftRotateTest(){
    var i10 Int = 10
    var i12 Int = 12

    rbtree := New()

    x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
    rbtree.root = x
    y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
    rbtree.root.Right = y

    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

    rbtree.LeftRotate(rbtree.root)
    
    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

}

func RightRotateTest(){
    var i10 Int = 10
    var i12 Int = 12
    
    rbtree := New()

    x := &Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, BLACK, i10}
    rbtree.root = x
    y := &Node{rbtree.root.Right, rbtree.NIL, rbtree.NIL, RED, i12}
    rbtree.root.Left = y

    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

    rbtree.RightRotate(rbtree.root)
    
    log.Println("root : ", rbtree.root)
    log.Println("left : ", rbtree.root.Left)
    log.Println("right : ", rbtree.root.Right)

}

func ItemTest(){
    var itype1 Int = 10
    var itype2 Int = 12

    log.Println(itype1.Less(itype2))


    var strtype1 String = "sola"
    var strtype2 String = "ailumiyana"

    log.Println(strtype1.Less(strtype2))
}

func InsertTest(){
    rbtree := New()

    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(10)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(9)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(8)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(6)})
    rbtree.Insert(&Node{rbtree.NIL, rbtree.NIL, rbtree.NIL, RED, Int(7)})

    log.Println("rbtree counts : ", rbtree.count)

    log.Println("------ ", rbtree.root.Item)
    log.Println("----", rbtree.root.Left.Item, "---", rbtree.root.Right.Item)
    log.Println("--", rbtree.root.Left.Left.Item, "-", rbtree.root.Left.Right.Item)

}


func main()  {
    log.Println(" ---- main ------ ")
    LeftRotateTest()
    RightRotateTest()
    ItemTest()
    InsertTest()
}

小结

好了本文 对红黑树的讲解到此结束，刚开始看红黑树的时候这些性质确实特别绕，但是理解了这5点性质，就好多了。 然后就是两个操作 ： 变色和旋转 理解红黑树是通过他们进行自平衡的就行了。
由于时间原因只写了插入了 ，没做删除，有机会再补上吧，不过理解了插入原理，删除也不在话下了吧。

有疑问加站长微信联系（非本文作者）

本文来自：博客园

感谢作者：ailumiyana

查看原文：红黑树原理详解及golang实现

入群交流（和以上内容无关）：加入Go大咖交流群，或添加微信：liuxiaoyan-s 备注：入群；或加QQ群：692541889

1419 次点击  
加入收藏 微博
赞
收入我的专栏
上一篇：如何客观的评价 Go 语言
下一篇：深度解密Go语言之 map
  • 类型定义
  • 代码
  • 变黑
  • 右旋
    0 回复
    暂无回复
    添加一条新回复 （您需要 登录 后才能回复 没有账号 ？）
    • 请尽量让自己的回复能够对别人有帮助
    • 支持 Markdown 格式, **粗体**、~~删除线~~、`单行代码`
    • 支持 @ 本站用户；支持表情（输入 : 提示），见 Emoji cheat sheet
    • 图片支持拖拽、截图粘贴等方式上传

    用户登录

    Go今日面试题

     今日阅读排行

      加载中

     一周阅读排行

      加载中

      关注我

    • 扫码关注领全套学习资料 关注微信公众号
    • 加入 QQ 群：
      • 192706294（已满）
      • 731990104（已满）
      • 798786647（已满）
      • 729884609（已满）
      • 977810755（已满）
      • 815126783（已满）
      • 812540095（已满）
      • 1006366459（已满）
      • 692541889

    • 关注微信公众号
    • 加入微信群：liuxiaoyan-s，备注入群
    • 也欢迎加入知识星球 Go粉丝们（免费）